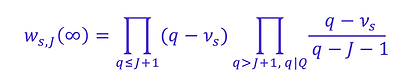Results for gaps in the sieve
From the models for relative populations of gaps across the cycles of gaps G(q#) as Eratosthenes sieve continues, we can derive several results in line with open conjectures about gaps between primes:
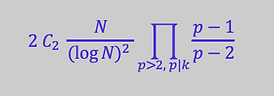
Twin primes & Polignac's conjecture
Twin Prime Conjecture
that there are an infinite number of pairs of consecutive primes that differ by the gap g=2.
Polignac's Conjecture
that for every even number 2k, there are an infinite number of pairs of consecutive primes that differ by the gap g=2k.
Hardy & Littlewood's Conjecture B
that the number of gaps g=2k between pairs of primes up to N should be approximately
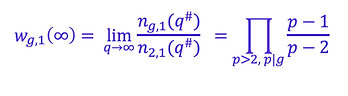
We show: the population of gaps g=2 in the cycles G(q#) grows by factors of (q-2), and for any other gap g=2k, its asymptotic relative population is given by
Admissible constellations & consecutive primes in arithmetic progression
k-tuple Conjecture
that every admissible constellation occurs infinitely often among consecutive primes
Hardy & Littlewood's Conjecture X1
that every admissible constellation s of length k-1 occurs infinitely often among primes and the number of occurrences of s up to N is approximately
where r is the number of residues mod p covered by s.
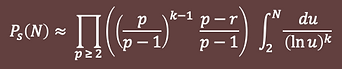
We show:
-
Every admissible constellation arises and persists in the cycles of gaps G(q#).
-
Let s be an admissible constellation of length J, and let Q be the product of odd primes that divide a span within s, then s has asymptotic relative population of
-
Consecutive Primes in Arithmetic Progression. An admissible repetition of a gap s= g g ... g of length J, corresponding to J+1 consecutive primes in arithmetic progression, has asymptotic relative population